Work-Stealing & Recursive Partitioning with Fork/Join

By on February 29, 2012

Implementing an efficient parallel algorithm is, unfortunately, still a non-trivial task in most languages: we need to determine how to partition the problem, determine the optimal level of parallelism, and finally build an implementation with minimal synchronization. This last bit is especially critical since as Amdahl's law tells us: "the speedup of a program using multiple processors in parallel computing is limited by the time needed for the sequential fraction of the program".

The Fork/Join framework (JSR 166) in JDK7 implements a clever work-stealing technique for parallel execution that is worth learning about - even if you are not a JDK user. Optimized for parallelizing divide-and-conquer (and map-reduce) algorithms it abstracts all the CPU scheduling and work balancing behind a simple to use API.

Load Balancing vs. Synchronization

One of the key challenges in parallelizing any type of workload is the partitioning step: ideally we want to partition the work such that every piece will take the exact same amount of time. In reality, we often have to guess at what the partition should be, which means that some parts of the problem will take longer, either because of the inefficient partitioning scheme, or due to some other, unanticipated reasons (e.g. external service, slow disk access, etc).

This is where work-stealing comes in. If some of the CPU cores finish their jobs early, then we want them to help to finish the problem. However, now we have to be careful: trying to "steal" work from another worker will require synchronization, which will slowdown the processing. Hence, we want work-stealing, but with minimal synchronization - think back to Amdahl's law.

Fork/Join Work-Stealing

The Fork-Join framework (docs) solves this problem in a clever way: recursive job partitioning, and a double-ended queue (deque) structure for holding the tasks.

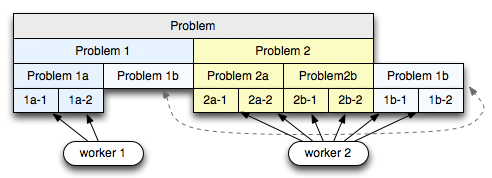
Given a problem, we divide the problem into N large pieces, and hand each piece to one of the workers (2 in the diagram above). Each worker then recursively subdivides the first problem at the head of the deque and appends the split tasks to the head of the same deque. After a few iterations we will end up with some number of smaller tasks at the front of the deque, and a few larger and yet to be partitioned tasks on end. So far so good, but what do we get?

Imagine the second worker has finished all of its work, while the first worker is busy. To minimize synchronization the second worker grabs a job from the end of the deque (hence the reason for efficient head and tail access). By doing so, it will get the largest available block of work, allowing it to minimize the number of times it has to interact with the other worker (aka, minimize synchronization). Simple, but a very clever technique!

Fork-Join in Practice (JRuby)

It is important to understand why and how the Fork/Join framework works under the hood, but the best part is that the API presented to the developer completely abstracts all of these details. The runtime can and will determine the level of parallelism, as well as handle all the work of balancing tasks across the available workers:

require 'forkjoin'

class Fibonacci < ForkJoin::Task
  def initialize(n)
    @n = n
  end

  def call
    return @n if @n <= 1

    (f = Fibonacci.new(@n - 1)).fork
    Fibonacci.new(@n - 2).call + f.join
  end
end

n = ARGV.shift.to_i
pool = ForkJoin::Pool.new # 2,4,8, ...

puts "fib(#{n}) = #{pool.invoke(Fibonacci.new(n))}, parallelism = #{pool.parallelism}"

# $> ruby fib.rb 33

The JRuby forkjoin gem is a simple wrapper for the Java API. In the example above, we instatiate a ForkJoin::Pool and call invoke passing it our Fibonacci problem. The Fibonacci problem is type of ForkJoin::Task, which implements a recursive call method: if the problem is "too big", then we split it into two parts, one of which is "forked" (pushed onto the head of the deque), and the second half we invoke immediately. The final answer is the sum of the two tasks.

By default, the ForkJoin::Pool will allocate the same number of threads as available CPU cores - in my case, that happens to be 2, but the code above will automatically scale up to the number of available cores! Copy the code, run it, and you will see all of your available resources light up under load.

Map-Reduce and Fork-Join

The recursion of the divide-and-conquer technique is what enables the efficient deque work-stealing. However, it is interesting to note that the "map-reduce" workflow is simply a special case of this pattern. Instead of recursively partitioning the problem, the map-reduce algorithm will subdivide the problem upfront. This, in turn, means that in the case of an unbalanced workload we are likely to steal finer-grained tasks, which will also lead to more need for synchronization - if you can partition the problem recursively, do so!

require 'zlib'
require 'forkjoin'
require 'archive/tar/minitar'

pool = ForkJoin::Pool.new

jobs = Dir[ARGV[0].chomp('/') + '/*'].map do |dir|
  Proc.new do
    puts "Threads: #{pool.active_thread_count}, #{Thread.current} processing: #{dir}"

    backup = "/tmp/backup/#{File.basename(dir)}.tgz"
    tgz = Zlib::GzipWriter.new(File.open(backup, 'wb'))
    Archive::Tar::Minitar.pack(dir, tgz)

    File.size(backup)
  end
end

results = pool.invoke_all(jobs).map(&:get)
puts "Created #{results.size} backup archives, total bytes: #{results.reduce(:+)}"

# $> ruby backup.rb /home/igrigorik/

The above is a simple, map-reduce example via the same API. Given a path, this program will iterate over all files and folders, create all the backup tasks upfront, and finally invoke them to create the backup archives. Best of all, there is no threadpool management or synchronization code to be seen and the framework will easily pin all of your available cores, as well as automatically balance the work between all of the workers.

Parallel Java & Distributed Work-Stealing

The Fork/Join framework is deceivingly simple on the surface, but as usual, the devil is in the details when it comes to optimizing for performance. However, regardless of whether you are a JDK user or not, the deque, combined with a recursive partitioning step is a great pattern to keep in mind. The JDK implementation is built for "within single JVM" workloads, but a similar pattern can be just as useful in many distributed cases.

Ilya GrigorikIlya Grigorik is a web ecosystem engineer, author of High Performance Browser Networking (O'Reilly), and Principal Engineer at Shopify — follow on Twitter.